1.緒言

地震予知に関する研究は，地震活動，地殻変動，地下水，電磁界変動などの多方面において実施され，且つ時間的にも直前，短期，長期と，多彩な探求が行われてきた (例えば, Rikitake, 1987; 吉田・古屋,　1992) ．それにもかかわらず，本来の意味で地震予知が成功したのは，中国の海城地震 (Wu et al., 1976) とメキシコの1978 Oaxaca地震 (Ohtake et al., 1981) だけで，それ以外には顕著な成功例がなく，地震予知そのものが不可能であるとの見方もある (例えば,　Geller, 1991) ．【活動実績4_Project1】

我々は，ボアホールを使った電磁界観測により東北地震の8日前からの記録で地震発生の1週間ほど前にULF帯 (ほぼ400 Hz) の現象 (マイクロクラック) が発生し，直前予知に使える可能性があることを示した (Fujinawa et al., 2013，Fujinawa and Noda，2020) ．しかし，その観測網が整備されておらず，実用化は期待されない。

他方，地震活動による研究は，観測網の整備がなされていることから，多面的な研究がされている (例えば, Jones and Molnar, 1979;吉田・古屋，1992; Scholz, 2002; Tamaribuchi et al., 2018)． 我々の経験でも地震直前の数日前に顕著な微小破壊を検知していることから，研究対象を直前の極微小地震（公式カタログに載らないほど小さい微小地震）と高周波微動に的を絞ることとした．

地震観測データは、防災科学技術研究所 (NIED)の高精度地震観測 (Hi―net) データを使うこととした．NIEDの連続観測網は，高精度な観測施設で，日本全国に隙間なく約800観測点が整備・運営されている (Okada et al., 2004) ．サンプリング間隔100 Hz, 24時間連続観測を行っており，地震研究への貢献は計り知れない．特に，連続記録データを基にし，Obara et al. (2004) により発見されたスロースリップに伴う低周波微動の現象は，大地震の予知のため，精力的な研究の対象となっている (例えば，Kubo and Nishikawa, 2020)．

我々は，Hi-net の原データを使い，可能な限り全ての極微小地震，高周波微動などのイベントを調べ，“高周波微動等カタログ”を作成しこれらのイベントが地震発生直前に，異常発生するのか否か，地震予知に役に立つ情報をどう引き出すかついて調べ，実用に供せる方法を提示する．

2.方法

2.1 対象イベント

使用する観測データは，NIEDのHi-net 観測データベースからダウンロードした．まず2011東北地方太平洋沖地震 (東北地震) の際に電磁界観測に使用していた神栖など茨木県北東部での観測点を初期調査のために選んだ．ちなみに，東北地震の破壊の西端が神栖に及んでいた (Fujinawa et al., 2013)．地震データの解析は，まずNIEDが公開している1ページ1時間の可視記録一か月分を目視で精査することから始めた．

それらの高周波微動イベントの特徴を定量化し，自動検出して特別カタログを作成した．地震直前の1週間に目立って発生・増大するイベントを抽出し，カタログを作成した．選んだイベントがカタログに含まれているか否かを目視で確かめ，数度にわたり抽出イベントの特性値を更新し完成させた．なお，気象庁， NIEDのカタログに含まれている地震によるものと判断される場合には登録されない．

これらの高周波微動等のイベントの特性を，継続時間，強度，周波数により定義した．当初は，以下の4種類のイベントを選んだ．

i.極微小地震：本来の地震であるが，小さくて公式カタログに記載されていない地震，
ii.脈動：長期連続 (数時間以上) 的に発生し，強度に時間変動がある (周波数0.5 Hz程度，スペクトル強度1 (μm/s) 2程度),
iii.高周波微動：脈動と同じく長期連続 (数時間以上) 的に発生している，卓越周波数は高く3帯域 (3, 10, 40 Hz) に分かれる微動，
iv.遠地地震：P波成分が減衰し，S波あるいはそれに似た波形を有する地震，

このような分類で，2011年の東北地震につき，北は青森県，南は千葉県までのHi-net 28観測点を選び，地震直前の1カ月特に地震直前1週間でそれらが顕著に増大しているかを目視で調べた．その結果，地震の直前に幾つかの観測点で，確かに本来の地震でない微動・地震イベントが複数種あることを確かめることができた．

然し，広大な地域であり，多様性に富んでいることから解析に困難を来たし，より単純と思われるM7クラスの地震 (2016熊本地震) を新たにサンプル地震と探索をした．

公開されている震源域 (気象庁・気象研究所，2016) を参照して，評価域を定め，域内20点の観測点を選び，データのダウンロードを行い，前項の定義で定めたイベントを抽出し，カタログ化した．何回かの試行錯誤の後，最終的に以下の特徴で規定される2種の微小地震と4種の高周波微動イベント (高周波微動等イベント：HFTs) などを選んだ．

No.1 近地極微小地震：P波とS波が明瞭で通常の地震そのものの極微小地震.
(特徴): P波成分 (高周波) とS波成分 (低周波) が明瞭．継続時間は5秒程度と短い．周波数帯は (2~30 Hz), ピーク周波数は，2~20 Hz.

No.2 遠地極微小地震：やや遠地の極微小地震で，高周波成分が減衰し低周波成分が卓越.
(特徴）: 高周波成分が小さく，ほとんど低周波成分のみで，継続時間は5秒程度と短い，周波数帯は (7~20 Hz),　ピーク周波数は，6~15 Hz.

No.3 近地高周波的地震 (紐型)：高周波微動の一部のような高周波微動イベント，
(特徴) : 紐状をなす, 初動 (P波) が明瞭，主要動 (S相) が不明瞭. 継続時間は10数秒とやや長い．周波数帯は2~40 Hz,　ピー ク周波数は3~20 Hz.

No.4 近地高周波的微動 (群発型)：変動が極めて大きく高周波微動の一部のようなイベント.
(特徴) : 群発的発生，初動 (P相)が不明瞭，主要動 (S相) は明瞭．高周波微動と混在し，地震直前では連続的に大発生する．周波数帯 (2~20 Hz), ピーク周波数 (3~20 Hz).

No.5 遠地高周波的微動：やや遠地の高周波的地震 (微動)で，高周波成分が減衰し低周波成分が卓越．
(特徴）: 高周波成分が殆どなく，低周波成分が卓越．継続時間は10数秒とやや長い．周波数帯は，2~15 Hz, ピー ク周波数は4~5 Hz.

No.6 複合高周波的微動：イベントNo.3の変形,
(特徴) : 継続時間が最も長く (30秒)，振幅の変動が極く小さい高周波微動イベント．

　この選択は，東北地震，熊本地震の各４観測点のデータを使い定めた．ちなみに全てのイベントの周波数帯は最小でも数 Hzで，スロースリップに伴う低周波微動 (Obara et al., 2004) に比べ高周波数帯の現象であり，また継続時間は30秒以内で低周波微動とは，殆ど重なっていない．イベントの波形例をとして，図1に，No.3の近地高周波的地震 (紐型) と No.4近地高周波的微動 (群発型) の波形を示す．

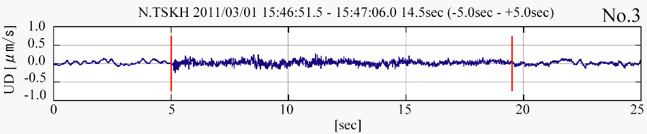
図1　地震発生のまえに発生する2高周波微動の波形

2.2 解析方法

過去に発生した大地震である熊本地震 (Mj 7.3, 2016/4/16 01:25)，新潟県中越沖地震 ( Mj 6.8, 2007/7/16 10:13) 及び岩手県内陸南部地震 (Mj 7.2, 2007/7/16 10:13) を例にとり，高周波微動等イベントの1時間ごとの発生数を基本データとした．評価域は震央を中心として震央距離の小さい順に20点の観測点が入る円形の領域とし，評価域の周辺に20 kmの分離帯を設け，その外側に同じく20点の地震観測点が入る領域を参照域として選んだ．

熊本地震の場合には，評価域 (主に熊本県) で20 点，評価域の周辺で20点合わせて40点である．なお，熊本地震の場合には，当初解析期間を本震前までとしたが本震と大きな前震の間の期間で高周波微動等の活動に，前震による余震の影響がある可能性があり，解析対象期間を前震までとした．ちなみに，気象庁・気象研 (2016)では，熊本地震では，本震と直前の前震を含め一連の地震群を一体化して扱っている．前兆現象のための解析期間は，2カ月間である．

2.3 イベント発生

熊本地震発生前1カ月間の評価域での20観測点における高周波微動等イベントごと発生数を調べてみた．イベントNo.1 ~ No.6の総和，分類ごとに一か月間の発生数を算定した．対象とする高周波微動等6種の内では，No.5の遠地高周波がほとんどの観測点 (16地点) で1，2位となっており，近地極微小地震 No.１が11 地点で1または2 位を占めていることも注目される．また，観測点ごとのイベント数には最大約30倍，イベントごとの差は最大100倍ほどの大きな差がある．そのため，各観測点の活動度の定義に工夫が必要である．

2.4 異常活動判定の閾値

　各イベントの発生数を1時間ごとに求め高周波微動等の基本指標とした．かなり大きな日周期などの環境ノイズの除去のために3日間の移動平均をとり，その結果を12時間ごとにサンプルし，時間 t での発生数を xij(t) とした．観測点iにおける高周波微動等イベント j ごとに，観測期間2カ月の内，地震直前の計測期間 (一か月間) の平均値をMij，標準偏差をσijとし，任意のサンプルデータの発生数の異常判定の閾値 NCij を次のように定めた，

NCij　=  Mij + 1.3*σij　　 (1)

観測点 i イベント j の時系列を，式 (1)で規定する閾値と比較し，観測値がそれを超えるときは，閾値越えとし，”1”を，閾値越えしない場合，”0”を付与し，その観測点の地震イベントの時間 t での活動度を定量化し，“スコア”と名づける．

スコアが1の場合，異常を「感知」したと定義する．この閾値を感知閾値とし，スコアは任意の時間，観測点での高周波微動等の活動が異常であるか否かを示すものとする．スコアは，地震イベント毎の発生数が観測点で大きく異なることから，複数の現象の活動度を総合的に数量化するために導入したものである．

なお，任意の時間 t での評価域・参照域でのスコアの総和をそれぞれの区域での総スコア (total score) とする．なお，総スコアは，破壊核形成の研究で使われている限界半径以上のPatches 数 (Dietrich, 1986)と似ている．

3.結果

3.1 前兆現象候補

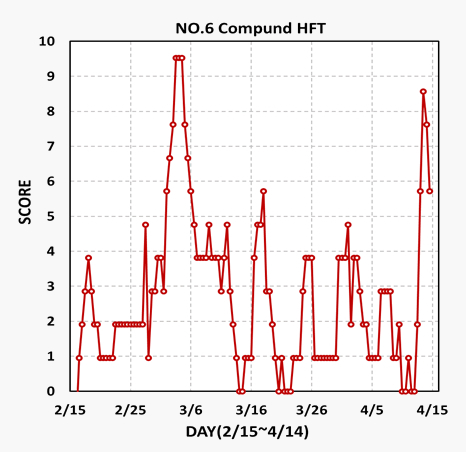
例として前兆現象を判別するうえで最も重要な役割を果たすこととなる3種の高周波微動等イベント6の時間変化を示す（図2）．解析表示期間は2016年2月15日から4月14日までの2カ月間で，総スコアが3 ~ 9のピークが5 ~ 10か所にある．まず比較的単純で地震直前の4月13日午後に顕著なピークがあることに注目する．合わせて，同じタイミングで，イベントNo.4も抜群に大きいスコア値9となっている．また，地震6週間前のピークは，3イベントともに最大となっている．

前震に関する研究 (Jones and Molnar,1979；Scholz, 2002) では，前震の単位時間当たりの数が地震直前に時間tの逆数 (1/t) 近い急激な増大があることが知られている．これらの結果を参照し，ここで定義した総スコアの地震直前の空間的な急速拡大も, “類似”の異常現象と考え，直前前兆現象候補とする．合わせて6週間前の明確なピークはスコア値と共に継続時間も最大であり，これを初期前兆現象候補とする．一方中間 (地震前ほぼ4週間前) のピークは明確でないが，ほぼ同じ時間にピークとなっており,中期前兆現象候補とした．

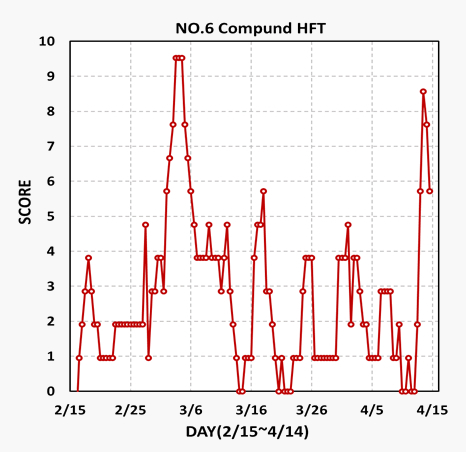
図2　高周波微動イベント (No.6) のスコアの地震前2か月間の変化

3.2 判別表

他方総スコアの時間変化を見ると，地震直前に大きなピークがある他，解析期間の初めに2番目に大きなピークがあり，その他の期間にも中ぐらいの大きさのピークが数個所に見られる．これらのピークには，1週間周期のノイズの影響もあると思われるが，地震直前などの主要ピークと区別ができないと“誤報”となるので，実用的な観点からは，主要3ピークそれぞれおよびその他のピークと判別ができなくてはならない．ピークの判別では，最大ピーク値に加え，一般破壊法則 (Fukuzono，1985; Voight, 1987; Jones and Molnar,1975; Scholz, 2002) を参照して，その時間微分 (加速度) を加えることとした．

判別表は，解析期間を5日間の区間 (1ピリオド) ごとに12に分けた（表２）．解析期間は，現段階では本震前の2か月間，地震発生後１か月間であるが，地震発生後は予知に関係がなく，イベントの活動度は地震直前より大きなものであるとの概要を把握するだけとした．判別表には，区間ごとの最大スコア，その時刻，スコア変化最大速度，を破壊域での高周波微動等イベント及びそれらの組み合わせ17種類イベントにつき記載される．　

3.3 判別結果

判別では，初期，中期，直前別に，ピーク値および増大値の閾値を定めた．閾値を定める条件としては，①評価域では3種の前兆現象が定まった時間順で検知されること，②参照域では，どの現象も検出されないこと，を条件とした．加えて，17種のイベント及びその組み合わせの内70%以上が一定のスコア(4.5)以上であり，一定の数以上のイベントが感知され信頼度が高いという条件を付した．

3.3.1 熊本地震

感知スコアの時系列を用い，ピークの第3共通判別法により，前兆現象か否かを判定した結果を，熊本地震の評価域{(a)Focal Area}・参照域別{(b)Focal Area} に求めたもの表2に示す．12のピリオドの内，判別に直接に係る3区間{初期(Initial)}, {中期(Intermediate)},{直前(Immediate}と{平穏時(Calm)} の代表的な区間だけが示されており，判別パラメータでは，判別に直接かかわるイベント (No.1~No.6) のみが記載されている．直前，中期，初期前兆現象を判別する条件にかかわる個所は，セルを赤色の数字で示してある．

表2　熊本地震の場合のイベント判別結果

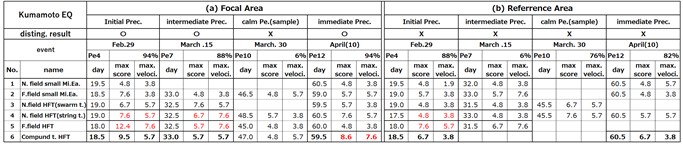
（1）評価域{表2，(a) Focal Area}, {直前前兆現象(Immediate)}
　2か月前からの解析では，イベントNo.6の最大のピークが第4ピリオド(Pe.4)，2番目に大きなのピークは第12ピリオド(Pe.12）に, 3番目のピークが第７ピリオドに出現している．イベントNo.6の判定閾値が (最大スコアPs, 最大速度Mv ) が (7,6)となっているのに対し，計測結果では (9,8) となっており，直前前兆現象として判別していることが分かる(赤字)．判別できたのは，前震の1.5日前，本震の2.7日前であった．

（2）評価域 {中期前兆現象 (Intermediate)}
　主要ピークの3番目に大きなのピークは，第7ピリオド (Pe.7)に出現した．これは，判別のための条件・閾値を満たしている．すなわち，表2の(a)評価域にあるように，イベントNo.4,5が中期前兆現象の条件を満たし，No.6 が最大スコア 6以下で直前現象でないと判別され，初期前兆の条件も満たしていない．地震は14日21時26分に発生したが，ほぼ 4週間前に中期予知情報として利用できることが分かる．

（3）評価域{初期前兆現象 (Initial)}
　初期のピークは，3大ピークの中で最大で，No.6が直前前兆の条件も満たしているが，3主要イベントの大小も勘案した判別条件となっているので，初期前兆現象と判別されている．

（4）参照域{表2，(b) Reference Area}, {直前前兆現象(Immediate)}
　熊本地震の参照域での地震 (前震) の前2カ月の高周波微動等の活動の異常判定の結果である．最も関心のあるのは，地震発生直前 (Pe12) に評価域での判定結果とどう異なるかである．参照域では，主要イベントNo.6の最大速度が閾値を超すが最大スコアが閾値7に達していない．また平穏時 (例えば，Pe.10) では，イベントNo.3は両閾値を超しているが，主要イベントに含まれていなく，参照域では地震発生はないと判別されている．また，中期・初期前兆現象の条件も満たしていない．さらに，判別されたイベントの信頼度は，初期94%,　中期88%,　直前94%で，条件を満たしている.

 これらの結果から，評価域では3種の前兆現象が判別でき，その都度発生時間が予測できることとなる．

3.3.2 新潟中越沖地震・岩手宮城内陸地震

　判別のための閾値は，現在のところ，経験的にしか求まらない．実際には，最初に解析した熊本地震の場合の判別条件を，第2サンプルの新潟中越沖地震にあてはめ，判別条件を調整し，2サンプル地震が同じ条件で適合できるような“第2共通判別条件”を求める．さらに第3の岩手県内陸地震を加え，第3共通判定条件を求めた．3大ピークの特徴が熊本地震の場合とよく似ているため，第2判別法が第1判別法とよく似ており，判別結果が熊本地震の結果 とよく似ている．

　岩手宮城内陸地震(2007) を合わせた3サンプル地震の第3共通判別法による判別の結果は，前2地震と同じよう結果となることから，詳細な説明は省略する.

3.3.3 推定時間

　熊本地震・新潟地震・岩手県内陸地震のM7クラス3地震の評価域・参照域合わせて6域での，地震前2カ月の異常判定結果を使い，地震直前を予測できか否か，地震直前以外の異常活動と区別できるかを調べ，直前前兆現象と共に，ほぼ4週間前に活発な活動 (中期予測)，6週間前に初期前兆現象が検知されることが分かった．また，初期前兆現象は地震の前6.4±1.2週間に検知され, 中期前兆現象は 4.6±0.4, 直前前兆現象は 0.5±0.3 週間前に検知されることが示された．

3.3.4 マグニチュード

　解析したM7クラスの地震3地震のそれぞれ3種の前兆現象において，ピークスコアから，HTFs が占める平面空間の面積が求まる．地震活動の空間分布の面積Sから，本震の地震規模Mを求める経験式(宇津・関，1955）では，M = LOG10(S)+4 が知られている．それを参照し，HFTs の分布面積S* からマグニチュードM* を求める実験式を, C を定数として，M* =  LOG10(S*) + C　と作成した． 最大級3ピークの内，最もスコアが大きいのは初期前兆現象であり，中でも主要3イベントの中でイベントNo.5 であるので，それを選んだ．そのスコアPs(5) から面積を求めるには，Hi-net観測網の格子間隔がほぼ20 kmである (Okada et al.,2002) ことを使うと，S* = Ps(5)*(20*20) と表わされる．地震活動を使った経験則を参照し，分布面積S*を求め，3地震のM*が実際の値に近くなるように，定数Cを求めると，M* =  LOG10(S*)+3.4となる．実測値との差 (ΔM*)は，±0.3となる．

3.3.5 震央位置

　予知の3要素の3番目は，地震の発生する場所である．スコアが1の観測点（感知点）の重心をつかい，3種の前兆現象を使って求めた．誤差は (±0.4°E, ±0.4°N) であり，実用に耐える範囲であると考えられる．なお，他の2種の前兆現象 (中期，直前) を使った場合は，誤差は，(±0.4°E, ±0.2°N),  (±0.4°E, ±0.3°N) と，殆ど同じである．3種の前兆現象が判別されるたびに発生場所が推定・確認できることとなる．

4.議論

4.1 破壊核形成

　検出した現象は，室内実験の結果に基づいた破壊核形成過程の研究結果特に断層滑り破壊モデルを参考にすると，理解できる．そのモデル (Dieterich, 1986; Das and Scholz, 1981; 大中, 1998) によると，テクトニック応力が増加する過程で，弾性限界を超えた段階から破壊核形成過程が始まり,ゆっくりした滑りと先行的地震活動たるHFTsが発生したと推定される．約6週間まえに，初期前兆現象と思われる異常なHFTsの活動が発生し，次いで中期前兆現象が発生，地震1週間前の直前前兆現象に対応する活動ピークを経て，数日の静穏期の後に本震発生となる．

 4.2 課題

解析時間が2か月としているが，2か月前に別の異常現象があり，抽出した3種の前兆現象と混同する可能性がある．これまでの前震に関する研究（Jones and Molnar, 1979; Scholtz, 2002)では，地震前1週間から50日未満に活動があるという事実からすると，高周波微動の活動が異なる可能性があり，検証する必要がある．

　また，あくまでもサンプル地震の範囲での判別法であり，未知の地震に対して，あてはまる保証はない．そのため，それぞれの前兆現象のなるべく一般的な特徴を把握して，リアルタイムモニターでは，過去の例を参照し，できるだけ正しい予測をするようにする必要がある．一般性の高い特徴としては，たとえば，初期前兆現象は，他の2種の前兆現象よりスコアが大きく，異常である時間がそれぞれ絶対的に大きいことがある．また，直前前兆現象では，ピーク幅が最も狭く，最大加速度が最大であるというロバストな特徴を勘案し，その時点の判別法で矛盾が出た場合，その時点で対応できるようにはなっている．

しかし，完全ではなく，なるべく多くのサンプル地震の結果を解析し，より一般性を有する判別法を開発すること，あるいはAI法による方法を応用する必要がある．

5.結論

　地震予知が実用化に至らない理由は，破壊核形成期に発生する現象が観測されないことから，定量的な議論ができないことにあると認識されている．そのため，高周波微動等イベントが短期地震予知に利用できないかを調べた．Hi-net連続観測網のデジタルデータを基に，微動など多くの振動現象を含む記録から地震直前に異常に多く発生する現象を探し,“高周波微動等カタログ”を作成した．

　イベントの活動状態の指標を，時間当たりの発生数とし，観測点・イベント毎に観測期間の統計値 (平均，分散) から，異常活動判定 (感知) のための閾値を定めた．観測点は、結果的に評価域で21点，評価域に隣接した参照域でも同じく21点の観測点を選び，評価域・参照域毎にデータを解析し，活動の異常度を示すスコアの時空間分布を求めた．

スコアのピークをピリオド (5日間) 毎に選び，それらのピークの内最大級の3ピークから，3種の前兆現象候補を選び，判別した．判別にあたり，地滑り，前震などの破壊現象に適応できる一般破壊法則を参照し，スコアとその時間微分を指標とした．M7クラスの3地震とやや小さい1地震をサンプルとして解析した．

　その結果，本震の発生直前(約１週間前 (0.5±0.3w) の“直前前兆現象”，ほぼ4週間前 (4.6±0.4w) の”中期前兆現象”，約6週間前 (6.4±1.2w) の“初期前兆現象”を判別できた．各前兆現象の検知時刻から本震発生時間を，観測点の分布面積からマグニチュードM (±0.3) を，検知観測点の平均位置から震央(±0.4°) を，実用に供する精度で推定できることが分かった．

また高周波微動等が，地震発生前の破壊核形成過程の前期における安定的かつ準静的破壊フェーズでのアスペリティの破壊に伴うものであると推定された．しかしながら，本フィルターでは，破壊核形成過程後期 (発生前約0.5w以降) の加速フェーズ・急速破壊進行フェーズは，検出できなかった．